Als in de 20ste eeuw Arnold Schönberg de 12-toons muziek introduceert, is de basis van de muziek niet meer de diatonische toonladder maar de chromatische. Omdat de tot dan toe gangbare opvatting van harmonie is gebaseerd op op de diatonische toonladder ontstaat er een harmonisch vacuüm. Peter Schat trachtte dit vacuüm op te vullen en ontwikkelde de toonklok, een inventarisatie van drieklanken in de chromatische toonladder. Onder drieklank wordt dan verstaan iedere mogelijke combinatie van drie intervallen. De definitie van drieklank is in deze duidelijk een andere dan de tot op dat moment gangbare. De akkoorden in de diatonische harmonie zijn immers opgebouwd uit tertsenstapelingen; de terts is dus de kleinste harmonische eenheid. Schat maakte de kleine secunde tot kleinste harmonische eenheid, wat logisch is als je chromatiek als uitgangspunt neemt.
Een inventarisatie van drieklanken in de chromatische toonladder, waarbij ieder cijfer staat voor het aantal halve tonen waaruit het interval bestaat, levert het volgende op:
1-1-10, 1-2-9, 1-3-8, 1-4-7, 1-5-6, 1-6-5........?
De laatste combinatie van intervallen hebben we al gehad in een andere volgorde, dus zoeken we de eerstvolgende
combinatie die we nog niet gehad hebben en gaan op dezelfde manier door:
2-2-8, 2-3-7, 2-4-6, 2-5-5, 3-3-6, 3-4-5, 4-4-4.
Dan blijkt dat er 12 verschillende drieklanken zijn; 12 verschillende combinaties van drie intervallen. Deze 12 drieklanken worden verdeeld over de 12 uren van een klok, in de hierboven genoemde volgorde.
Op ieder uur staat vervolgens een diagram dat vier complementaire drieklanken symboliseert. Deze diagrammen zijn ook gebaseerd op een klok; de chromatische tonen zijn genummerd van 1 tot 12 en zijn over de klok verdeeld; Dit levert deze module op: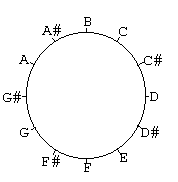 

Uur I bestaat uit de volgende 4 drieklanken : 123,456,789 en 10 11 12.
Als 1 een C is onstaan dan de volgende drieklanken: C-C#- D, D#-E-F, F#-G-As en A-A#-B. Het tweede uur bestaat uit een kleine secundes, grote secundes en grote sexten. Benoemen we deze op dezelfde manier dan is dat 1 2 4, 3 5 6, 7 8 10 en 9 11 12. Het twaalfde uur is gevuld met grote tertsen. "En," zei Peter Schat tegen mij "te elfder ure verschijnt Rameau...." Inderdaad, het elfde uur bestaat uit kleine tertsen, grote tertsen en reine kwarten; grote en kleine drieklanken (dit omdat een kleine drieklank een spiegeling is van een grote: grote terts/kleine terts/reine kwart en reine kwart/kleine terts/grote terts).
Tekenen we de drieklank C-E-G in de module: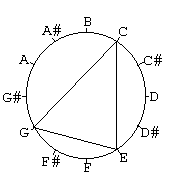 

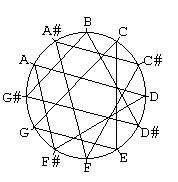
En in de volgende module zien we dat deze combinatie van intervallen vier keer in de module past.
Alle andere boven genoemde combinaties passen vier keer in de module, behalve de verminderde drieklank. Deze is afgebeeld als een verminderd septimeakkoord, en past drie keer in de module.
Plaatsen we alle modules nu op de uren van een klok, dan ontstaat de afbeelding van de toonklok. Ieder uur van de toonklok wordt weer gestuurd door een ander uur. Het volgende hoofdstuk geeft een overzicht van deze sturingen.